Okay, here is finally Part 3 of my "
modelling travel times for the Havelock alignment" exercise (refer back to Post
#7,315 for Part 2):
4. Model Solving
4.1 Ignoring s-curves
There is actually not that much left to say, apart from that the train movement is modelled in a way where the train stays to the applicable speed limits (and within its dynamic capabilities), which results in a speed profile similar to this one:
Quoted from:
my Master Thesis (p. 76)
Just like in my Master Thesis, my modelling will be based on the following parameters:
Design speed (as quoted numerous times by VIA) and acceleration/deceleration capabilities (discussed in
Part 1 of this series) are relatively straight forward and the recovery margins are taken straight from UIC recommendations (note that I had to change the distance-based recovery margin from 60 to 90 seconds compared to my Master Thesis, as VIA's future fleet will still be locomotive-hauled, but a "percentage running time supplement" of 5% still applies, as a 5-car trainset should fall into the 301-500 tons weight category):
Quoted from:
my Master Thesis (p. 34)
But why would the train length matter? Well, unlike speed limits for cars (or at least how motorists like to interpret them), a more permissive speed limit only takes effect after the whole train has passed the point where the higher speed limit applies. Therefore, the train is only allowed to accelerate once the last axle has left the zone in which the last (more restrictive) speed limit remained valid. I kept the value of 680 feet I used in my Master Thesis, as it represents 3 block lengths, which equals 241 meters (0.15 miles), thus enough to fit a 7-car train hauled by a locomotive (like the "Extra long trainset" representing the
longest-possible trainset configuration of VIA's future fleet) in its entirety.
4.2 Respecting s-curves
Even though I never rode a motorcycle, I've been told that taking a right curve followed immediately by a left curve gives you a good chance of finding yourself lying with your motorcycle on the side of the road and it is not much different with trains, as the superelevation applied to the track has the same function of a motorcyclist tilting his bike into a curve and it therefore takes a moment to transition from one curve in one direction into a curve in the opposing direction. The same issue arose to me when playing the game "Rollercoaster Tycoon 2" and where the virtual visitors of my park would refuse to board attractions which would expose them to too extreme lateral forces.
However, first we have to talk about transition curves: as we have seen in previous posts, the equilibrium superelevation is dependent on basically two variables: the radius of the curve and the banking of the track. This necessitates that in order for the outer (i.e. the "superelevated") rail to gently reach the same vertical level as the inner rail, the radius has to increase just as gently so that the track becomes straight again at exactly the point where the outer rail reaches the vertical level of the inner rail. Unfortunately, I'm no railway engineer and I never took any courses talking about the science of track alignments, but I found
this highly interesting presentation which provides formulae for the
easement (i.e. transition curve) length for both, the actual superelevation applied to the track (E_a) and the underbalance (E_u), of which of course the greater value applies as minimum value for a given curve:
Quoted from:
Lautala et Dick (2010, Slide 9)
Additionally, the same source describes the need a tangent (i.e. straight) track, with a minimum length of the greater of the distance covered in 3 seconds at the maximum applicable speed or (for very low speeds) 100 ft:
Quoted from:
Lautala et Dick (2010, Slide 11)
I would have liked to present the slides here, but got discouraged by the disclaimer on the final slide of the presentation. Nevertheless, I've linked the source and the presentation is easily accessible and - I repeat myself - highly interesting!
That said, I'm still trying to get my head around the specificities of s-curves (or
reverse curves) I outlined above, but it becomes clear that there are painful trade-offs between the amount of superelevation applied to curves and the maximum speed which can be achieved on the tangent between these curves (if the two curves form a reverse curve) and this means that achieving aggressive superelevations (like 8 or 10 inches) might be unrealistic on segments riddled with reverse curves (like this segment between Sharbot Lake and Mountain Grove) - a problem which (as a side note) tilting trains would not solve, as the extra banking needs to be treated the same way in the formulae presented above as the actual elevation applied to the tracks:
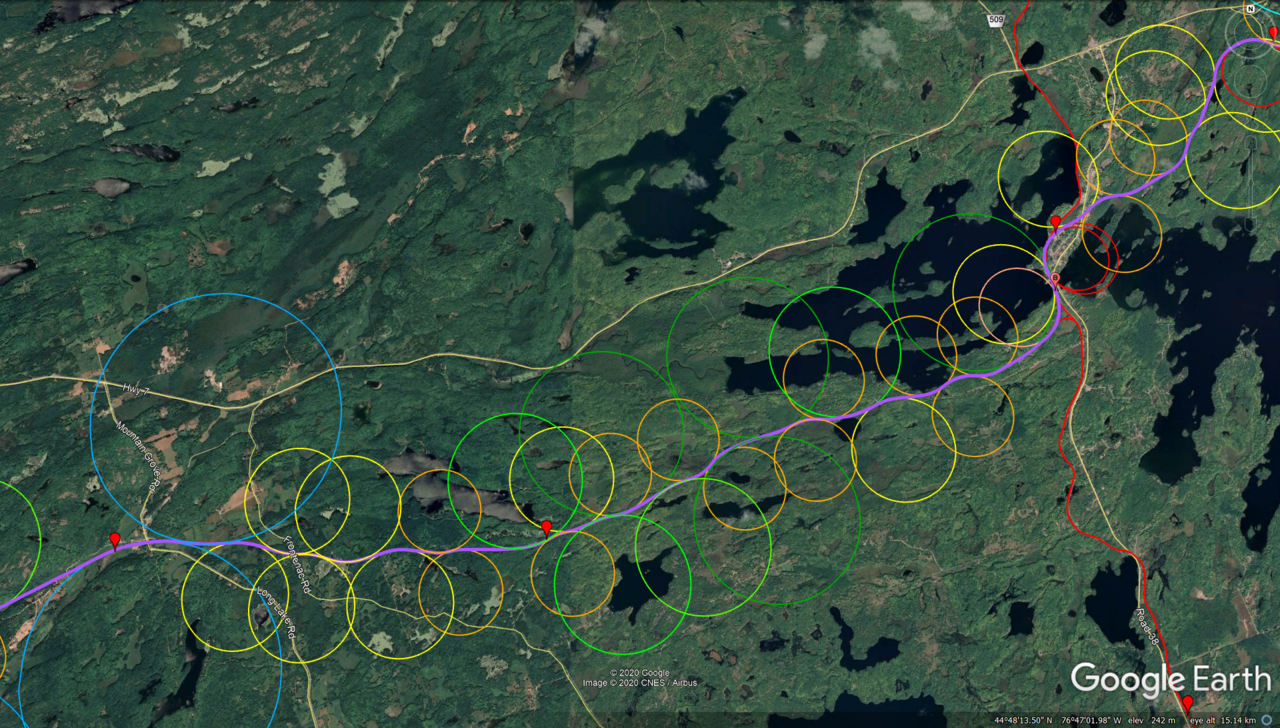
I hope you found this 3-part excurse into railway travel time modelling as instructive as I found it (I never thought that I would delve even deeper into this matter than I already did for my Master Thesis - but reverse curves really weren't that much of an issue on the Kitchener Corridor than they are on the Havelock Subdivision) and I will try to get my head around these pesky reverse curves and model travel times for the existing/former Havelock alignment, so that
@reaperexpress and
@crs1026 can take control of my spreadsheet and see what kinds of realignments may or may not be required to achieve a travel time of 3:15 hours between Toronto and Ottawa...
In the meanwhile, I wish you all a good night and have a great start into the new week!




